This states Investigate characteristics of parallel and perpendicular both algebraically and geometrically.
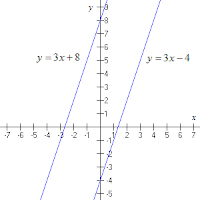
First I will show you geometrically:
Now the one to your left is perpendicular and the one to your right is parallel.
The perpendicular one has only one solution that is the point of intersection or where they meet. Also their slopes are negative reciprocals of each other. So lets say the slope is 6 the negative reciprocal of that is -1/6, because 6 is like saying 6/1.
The parallel lines have no solutions but their slopes are identical or the same.
Remember these things as I am about to explain this algebraically.
Say for instance you have your system and they are in slope y-intercept form:
y=5x-2,y=5x+3 The lines will be parallel because their slopes are the same AND THEIR Y-INTERCEPTS ARE DIFFERENT. For if they have the same slope and y-intercept it is one line and the solution set is infinite, but this does not apply for perpendicular lines. Okay, you have
y=-5x-9, y=1/5x-9 it is perpendicular because the slopes are negative reciprocals of each other, and making one solution. In some cases you with have to rewrite to figure out what they are.

You will have to remember all rules in order to understand this.
ReplyDelete